top of page
Difficile de faire plus simple : une seule pièce d'habitation et un toit plat.
Dimensions extérieures : environ 45 x 54 x 33 mm.
Quatre ouvertures dont une porte.
... et c'est tout.
Plus modeste, on peut pas.
Les murs ont une épaisseur de 3 mm.


Difficile de faire plus simple : une seule pièce d'habitation et un toit plat.
Dimensions extérieures : environ 45 x 54 x 33 mm.
Quatre ouvertures dont une porte.
... et c'est tout.
Plus modeste, on peut pas.
Les murs ont une épaisseur de 3 mm.
Pour imprimer cette petite maison j'ai choisi du fil PolyWood. C'est un PLA avec du bois qui donne à la pièce un aspect "bois mat" ou "terre sèche". Facile à enduire et à peindre.
Suivant l'imprimante utilisée, il sera nécessaire de réduire au papier de verre les dimensions du toit pour qu'il s'encastre correctement et vienne en appui sur les petites nervures qui ceinturent le bâtiment à l'intérieur des murs.
Pour éviter l'affaissement des linteaux l'impression est paramétrée avec "supports d'impression", c'est à dire que les porte et fenêtres (ben oui, ya qu'une porte ! ) seront remplies d'une sorte de nid d'abeille qui supportera les linteaux au moment de leur impression.
Il faudra ensuite désoperculer toutes les ouvertures pour les débarrasser de ces supports, puis ébavurer correctement.

La maison, avec son toit, et la porte partiellement désoperculée.
Note :
Cette petite maison peut être facilement imprimée à l'échelle "N".
Il suffit, dans CURA by Dagoma, d'utiliser les mêmes fichiers ".stl" et d'appliquer le coefficient de réduction 0,54. (Hé oui ! Pas besoin de redessiner).
L'impression prendra 20 minutes et 4 grammes de PLA pour un coût matière de l'ordre de 0,20€ !
Si l'échelle 1:43 vous tente, il suffit d'appliquer un coefficient x2 dans CURA.
Il faudra 5 heures d'impression et 73 grammes de PLA (moins de 4€).
C'est encore jouable.
Ah ! petite remarque : le bâtiment est marqué "HUGO 2017" à l'intérieur.
Mon petit fils voulait que "son œuvre" soit signée ! (c'est la seule chose que j'ai faite sur ce modèle).
Téléchargements :

Petite maison en adobe
Un de mes petits fils voulait absolument dessiner et imprimer une maison en 3D.
J'ai orienté son choix vers un modèle simple : une petite maison de paysan modeste de la région de Santa Fe, en adobe, qui va me servir sur mon réseau. Tant qu'à faire...
Table des matières
-
Préambule
-
Unités
-
Deux grandes familles de condensateurs
-
Représentations schématiques et notations
-
Gammes normalisées
-
Marquage et lecture
-
Constitution physique
-
Caractéristiques limites
-
Constante de temps d'un condensateur
-
Quantité d'énergie stockée dans un condensateur
-
Impédance d'un condensateur
-
Le condensateur utilisé comme réservoir d'énergie
-
Le condensateur utilisé pour «lisser» une tension redressée
-
Le condensateur utilisé comme antiparasite
-
Le condensateur utilisé comme élément d'un oscillateur
-
Le condensateur utilisé comme temporisateur
-
Le condensateur utilisé comme limiteur de courant
-
Association de condensateurs
Avant toutes choses je précise que l'étude des condensateurs est un TRÈS TRÈS vaste sujet.
Il n'est donc pas question de faire un exposé exhaustif qui nous entraînerait beaucoup trop loin.
Préambule
Préambule
Le condensateur est un composant électrique ou électronique conçu pour pouvoir emmagasiner une charge électrique importante (c'est-à-dire de l'énergie) sous un faible volume.
C'est un accumulateur d'énergie.
Unité
Unité
L'unité de capacité est le farad,
du nom du physicien et chimiste anglais Michael FARADAY.
Symbole : F
Cette unité est en pratique très grande.
On utilise usuellement ses sous-multiples (voir le "topo" sur les unités) :
-
microfarad (symbole : µF) ;
-
nanofarad (symbole : nF) ;
-
picofarad (symbole : pF).
Depuis quelques temps on a vu apparaître sur le marché des condensateurs de très fortes valeurs : plusieurs farads, voir plusieurs centaines de farads.
Pour mémoire, en considérant la Terre comme une sphère conductrice de 12 800 km de diamètre, on lui trouve une capacité de ≈710×10-6 farad (≈710 µF)
Comme tous les noms d'unités du Système international, « farad » s'écrit en minuscules .
En revanche, comme ce nom provient du patronyme d'un physicien , le symbole associé « F » s'écrit en majuscule.
J'ajoute que, le cas échéant, « farad » prend la marque du pluriel comme n'importe quel nom commun.
Note :
En France, la norme dit qu'une unité prend la marque du pluriel si et seulement si la quantité est supérieure ou égale à 2.
Par exemple : 3 farads ; 1 farad ; 1,5 farad ; 0,7 farad
Familles
Deux grandes familles de condensateurs
Condensateurs polarisés
Ces condensateurs sont sensibles à la polarité de la tension électrique qui leur est appliquée.
Ils ont une borne négative et une borne positive.
Ce sont essentiellement les condensateurs de technologie « électrolytique » (également appelée, par abus de langage, « chimique ») et « tantale ». (voir plus loin).
Une erreur de branchement ou une inversion accidentelle de la tension aux bornes conduit généralement à leur destruction, qui peut être très brutale, voire explosive, particulièrement sur des condensateurs de plusieurs farads.
Leurs valeurs s'échelonnent de 500 nanofarads à plus de 1000 farads (!) pour les derniers nés de la technologie moderne.
Condensateurs non polarisés
Ils ne sont pas sensibles à la polarité de la tension.
Leurs valeurs s'échelonnent de 1 picofarads (1 pF = 10^-12 F) à environ 10 microfarads (1 µF = 10^-6 F).
Ce sont donc plutôt des condensateurs de faible capacité, mais souvent avec une tension de service élevée.
Représentations
Représentations schématiques et notations
Les résistances ont une seule représentation schématique (sauf cas très spéciaux).
Les condensateurs, eux, sont représentés de différentes façons en fonction du logiciel que l'on utilise mais aussi de certaines habitudes "nationales".
Condensateurs non polarisés
En général, aucune ambiguïté : 2 traits parallèles et c'est tout.

Condensateurs polarisés

Représentations courantes.
La troisième ne se rencontre pratiquement plus.
Elle est pourtant claire et pratique.

Représentations dans le logiciel DesignSpark

Représentation dans le logiciel PROTEUS ISIS
Notations schématiques
Un condensateur, quel que soit son type, est usuellement noté "Cxx".
On indique la valeur de capacité ET la tension maximale de service.
La valeur de la capacité est habituellement indiquée de façons suivantes :
-
100 nF = 100.10^-9 F que l'on prononce «100 nanofarads» ;
-
100 n, (on omet le nom de l'unité et on se contente du préfixe, puisqu'il s'agit obligatoirement de farads) ;
-
47 pF ou 47 p = 47.10^-12 F que l'on prononce «47 picofarads» ;
-
4,7 nF ou 4,7n ou 4n7 que l'on prononce «4,7 nanofarads» ;
dans le 3e cas, la lettre « n » indique la position de la virgule ;
-
220 µF = 220.10^-6 F que l'on prononce «220 microfarads» ;
-
220 µ (on omet le nom de l'unité) ;
-
2,2 µF ou 2,2 µ ou 2µ2 = 2,2.10^-6 F que l'on prononce «2 virgule 2 microfarads» ;
Aussi simple que pour les résistances !
... ben pas vraiment...
Exceptions :
Sur les schémas, et même dans les calculs, on rencontre de façon très courante des notations surprenantes, pour ne pas dire exotiques.
Bien entendu certaines de ces notations sont erronées... mais elles existent et il faut savoir les décoder.
Exemples :
-
15 000 pF ou 15 000 p, alors qu'on aurait pu et dû écrire 15 nF. Jusque là, rien de grave.
-
4700 µF ou 4700 µ, alors qu'on aurait pu et dû écrire 4,7 mF (millifarad)
En fait, l'usage en électronique veut qu'on emploie le pico-, le nano-, le micro-farad... et le farad mais quasiment jamais le millifarad.
Encore plus fort : (vu sur ebay)

Pour les condensateurs électrolytiques on rencontre - surtout chez les américains - les notations
100uF, 100 UF, 100 MF en lieu et place de 100 µF !
Là par contre ça devient grave. Ils ont tout mis... Sauf la bonne notation !
-
en effet, le préfixe «M» existe mais il vaut 10^+6 ( et pas 10^-6 ) et il se prononce «méga» !!! (voir la table des préfixes).
La désignation 100 MF est donc une ineptie, même si il n'y a pas de doute quant au véritable ordre de grandeur de la valeur, puisqu'un condensateur de 100 mégafarads est impossible à fabriquer dans l'état actuel de la technologie.
Ah ! ces américains.
-
le préfixe «U» n'existe tout simplement pas !
-
le préfixe «u», lui, s'explique plus facilement : les claviers américains n'ont pas les lettres accentuées en direct, ni le caractère grec «µ», pourtant courant sur les claviers français.
Par commodité, «µ» est remplacé par «u» dans des logiciels d'origine anglosaxonne comme PROTEUS par exemple.
Donc, sur ce point, et sur ce point seulement, nos amis américains sont pardonnés.
Gammes
Gammes normalisées
Eh oui ! «Gammes» au pluriel.
J'avais prévenu : le condensateur, c'est pas simple !
Les séries «Exx» sont en principe associées à une tolérance de fabrication :
-
E3 : ±40 %,
-
E6 : ±20 %,
-
E12 : ±10 %,
-
E24 : ±5 %,
Ci-dessous un tableau résumé des séries les plus courantes :
_p.png)
Pourquoi une série E6 avec des valeurs aussi éloignées les unes des autres ? (chaque valeur vaut environ 50% de plus que la précédente).
Tout simplement parce pour certains types de condensateurs (électrolytiques en particulier. Voir ci-dessous), les technologies de fabrication conduisent à des écarts de valeurs importants par rapport à la valeur nominale visée.
Dans ce cas, les séries E12 ou E24 n'auraient aucun sens.
Condensateurs non polarisés :
Il s'agit des condensateurs de faible valeurs (souvent < 1 µF), de technologie non électrolytique (sauf exception très particulière).
Leurs tolérances de fabrication sont généralement de l'ordre de 10%.
La gamme des valeurs est donc généralement E12.
Condensateurs polarisés :
Ce sont les condensateurs électrolytiques ou les condensateurs "tantale".
Leurs tolérances de fabrication sont généralement de l'ordre de 20% à 50%.
La gamme des valeurs est donc généralement E6 et parfois E3.
Voir à ce sujet l'extrait "Wikipedia" de la norme CEI 60063 dont est extrait le tableau ci-dessus.
Marquage
Marquage et lecture
(Sous-titre : « Ici tout se complique »)
Il est déraisonnable d'essayer d'expliquer tous les types de marquages.
Cas simple : les condensateurs électrolytiques :




La capacité et la valeur limite de tension d'utilisation sont marquées «en clair».
La plupart du temps ces condensateurs sont assez volumineux pour permettre un marquage non codé.
Remarque :
Sur les condensateurs électrolytiques, la bande étroite de couleur différente marque la borne «moins», c'est-à-dire la cathode du condensateur, même lorsque le signe «moins» n'est pas indiqué.
Sur les deux condensateurs à droite, cette borne «moins» correspond aussi à la patte courte.
J'aime la simplicité des condensateurs électrolytiques !
Utilisation du codage couleurs :
Historiquement, les condensateurs électrolytiques de forte capacité (xxx microfarads) sont apparus bien après les condensateurs de faibles valeurs, plus faciles à fabriquer avec les technologies du début du XXème siècle.
Aux débuts de la radio on utilisait des condensateurs de quelques pico à quelques nanofarads non polarisés.
Les condensateurs de valeurs supérieures (quelques microfarads) étaient rares.
On a donc tout naturellement employé le picofarad comme unité de base pour caractériser la capacité des condensateurs.
Exemple n° 1 :
_p.png)
Le code couleur se lit de bas en haut.
Génial, non ?
Et encore, c'est le cas le plus simple.
Exemple n° 2 :
_p.png)
Comme il s'agit de condensateurs il est logique et quasi indispensable de préciser la tension de service.
C'est ce que fait la 5ème zone de couleur.
Ah, ben non... pas pour ceux ci-dessous...
NDLR : si vous trouvez un condensateur tout rouge avec des points noirs... c'est une coccinelle ! ;-)
Voici le tableau qui devrait permettre de décrypter les codes couleurs des condensateurs,
quel que soit leur type :

On constate déjà, dans les deux exemples précédents, que la pratique est souvent assez éloignée de la règle.
Exemple n° 3 :
_p.png)
Marquage « en clair » :
Ouf ! On va enfin y voir un peu plus clair !
Exemple n° 1 :
_p.png)
_p.png)
Presque tous les condensateurs plastiques de qualité courante, dans les valeurs de 1 à 1000 nF, sont marqués ainsi.
Que du bonheur !
Exemple n° 2 :
_p.png)
Exemple n° 3 :

Ahhh !
Cette notation apparaît soit seule (cas ci-contre), soit en double avec une inscription en clair de la valeur.
Capacité = 100nF
Si, si !
« 104 » c'est la valeur exprimée en « picofarads » !
104 correspond à 10 x 10^4, soit 100 x 10^3 picofarads,
càd 100 nanofarads.
Ce type de marquage s'apparente au marquage des résistances CMS :
-
2 chiffres pour la valeur ;
-
1 chiffre pour le multiplicateur.
... sauf qu'ici, l'unité de base est le « picofarad » et pas le « farad » !
Vous suivez ?
Marquage alphanumérique résumé
Indication de la capacité
47 : 47pF ou 47µF selon le type de condensateur. En général, il n'y a pas de doute possible
.47 : 0,47µF
4p7 : 4,7pF - le symbole p (n pour nano, u ou µ pour micro) marque la place du point décimal
47n : 47nF
n47 : 0,47nF = 470pF
4k7 : 4700pF - sur les condensateurs céramiques, la lettre k peut être un multiplicateur par 1000 !
104 : 10x10000 = 100nF - le 3ème chiffre représente le nombre de zéros à ajouter au nombre formé par les deux premiers chiffres.
4R7 : 4,7pF - un "R" remplace le point décimal (et pourtant, il ne s'agit pas d'une résistance ! )
R47 : 0,47pF (même remarque)
Indication de la tolérance
pas de tolérance indiquée ⇒ en général 20%
5% : 5%, sans aucun doute
.22 J 63 : 0,22µF - 5% (voir tableau alphabétique des tolérances ci-dessus) - 63V
220n K : 220nF = 0,22µF 10% (lettre K)
0,47/10 400V : 0,47µF 10% 400volts (le symbole % est souvent omis)
473K : 47nF 10%
Indication de la tension
.33 K 63 : 0,33µF 10% 63 volts (l'unité V est très souvent omise)
0,22/250 : 0,22µF 250 volts
0,01/10/160 : 10nF 10% 160 volts
4n7 K 100 : 4,7nF 10% 100 volts
561K63V : 560pF 10% 63 volts
500pF 500V- 200V~ : 500pF 500volts en continu et 200 volts en alternatif
100M1kV : 100pF 20% 1000 volts (1 kilo-volts)
... et pour finir, un premier piège :
« 330 » peut vouloir dire 33 pF (33 suivi d'aucun zéro, en codage chiffré) ou 330 pF (codage en clair) !
... et un deuxième piège :
« 479 » : écart de règle. La valeur est ici de 4,7 pF (47 divisé par 10) : le chiffre 9 ne signifie pas «9 zéros»,
mais «divisé par 10» !
Non, non, ne partez pas tout de suite...
Condensateurs « CMS »
Là le problème est encore plus compliqué.
Contrairement aux résistances CMS, les condensateurs CMS ne portent que très rarement un marquage !


Bien malin celui qui est capable de distinguer ces deux condensateurs « à l'œil » !
C'est même rigoureusement impossible.
Pourquoi une telle différence de traitement dans l'identification des condensateurs et des résistances ?
... d'autant que les condensateurs « tantale », eux, sont marqués.
Bon, d'accord, ils sont un peu plus gros, mais les résistances CMS 0603 sont très petites et pourtant elles sont marquées !
Voilà un grand mystère qui n'est pas près de trouver une explication.
Conclusion pratique
J'avais prévenu : avec les condensateurs, rien n'est simple !
DONC...
Un bon conseil :
Quand vous achetez des condensateurs de faibles valeurs, quel que soit leur type, ne perdez ni la boite, ni la facture !
Sans cette précaution, le stock de condensateurs sera vite un joyeux foutoir (pour rester poli).
Physique
Constitution physique des condensateurs
Un condensateur est formé de deux armatures conductrices (A) séparées par un isolant appelé diélectrique (D).
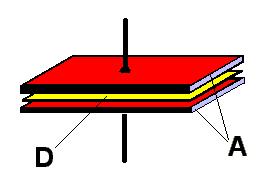
Le diélectrique peut être en verre, air, film plastique, mica, céramique, papier, alumine...
Pour faire simple :
-
plus la surface des armatures est grande, plus la capacité est importante ;
-
plus le diélectrique est mince, plus la capacité est importante ;
-
plus le diélectrique est mince, plus faible sera la tension de service. Mais cette tension de service dépend aussi de la qualité et de la nature du diélectrique.
Tout l'art consiste à trouver des technologies pour augmenter la surface des armatures, diminuer l'épaisseur du diélectrique et obtenir une tension de service et une capacité adéquates, des fuites faibles ainsi que des performances en terme de fréquence.
C'est ce qui explique le nombre important de types de condensateurs.
Caractéristiques
Caractéristiques des condensateurs
-
un condensateur est essentiellement caractérisé par la valeur de sa capacité, exprimée en farads, comme nous l'avons vu ci-dessus ;
-
une deuxième caractéristique très importante est la tension de service.
... mais ce n'est pas tout :
-
un condensateur peut être « polarisé » ou non.
-
la nature du diélectrique conditionne son domaine d'utilisation ( audio, radio-fréquences, filtrage, découplage, antiparasite, condensateur de démarrage, etc.).
Chaque modèle de condensateur est aussi caractérisé par :
-
une température de fonctionnement maximale ;
-
un taux d'humidité ambiante maximale ;
-
une tolérance de valeur ;
-
un courant de court-circuit maximal ;
-
une résistance série équivalente ;
-
un courant de fuite ;
-
etc.
Le non respect des limites d'utilisation peut conduire à de sérieux déboires, voir des accidents.
Quelques repères rapides concernant l'usage du condensateur
en fonction de la nature du diélectrique :
_p.png)
En fait, dans nos applications électroniques en modélisme, nous utilisons essentiellement trois types de condensateurs :
-
les condensateurs électrolytiques aluminium ;
-
les condensateurs à diélectrique plastique ;
-
les supercondensateurs.
Plus rarement on utilisera des condensateurs céramiques.
Constante de temps
La constante de temps
Un condensateur est un composant qui peut stocker de l'énergie, mais il ne se comporte pas comme une batterie : pendant la charge ou la décharge à travers une résistance, la tension aux bornes du condensateur varie de façon exponentielle.
Ci-dessous sont représentés les montages d'essai de charge et de décharge d'un condensateur, à travers une résistance :

Voici l'allure des courbes de charge (en bleu) et de décharge (en rouge) d'un condensateur :
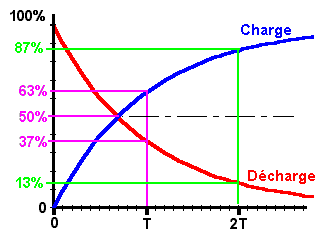
«T» est la fameuse constante de temps.
La charge (ou la décharge) du condensateur à travers la résistance n'est pas instantanée.
La constante de temps «T» est le temps nécessaire au condensateur pour :
-
se charger à 63% de la tension de l'alimentation ;
-
perdre 63 % de sa tension lors de la décharge, c'est-à-dire atteindre 37% de la tension de départ.
Note : «63%» est une valeur conventionnelle calculé ainsi : 1 - 1/e = 63%
«e» est appelée nombre d'Euler ou encore constante de Néper (deux mathématiciens).
«e» vaut 2,71828.
«e» sert de base aux logarithmes naturels, suivant la définition ln(e) = 1.
Comment calcule-t-on cette constante de temps ?
La constante de temps dépend uniquement de :
-
la valeur de la capacité du condensateur ;
-
la valeur de la résistance.
Elle ne dépend en aucun cas de la valeur de la tension de l'alimentation.
La formule de calcul est toute simple : T = R·C (T en secondes ; C en farads ; R en ohms)
(Le point «milieu de ligne» remplace le signe «x» )
Si on exprime la valeur de C en microfarads, la formule est : T = R·C / 1 000 000
Note :
Le temps 5T (5 fois la constante de temps) et la durée après laquelle on considère que le condensateur est soit complétement chargé, soit complétement déchargé.
En réalité, au bout du temps 5T, le condensateur est chargé à 99,3% (ou déchargé à 0,7%) de la tension de l'alimentation.
Quelques exemples de constantes de temps, juste pour fixer les idées :
R (ohms)
1 000 000
1 000
1 000
1 000
1 000
10
4 700
10 000
C (µF)
1
10
100
1 000
10 000
4 700
1 000
1 farad
T (en secondes)
1
0,01
0,1
1
10
0,047
4,7
10 000
(environ 3 heures)
5T
5
0,05
0,5
5
50
0,235
23,5
50 000
(14 heures)
Remarque :
On obtient la même constante de temps avec le couple [1 MΩ – 1 µF] et avec le couple [1000 Ω – 1000 µF].
Bonus
Ci-dessous, 2 petites vidéos qui simulent la charge et la décharge d'un condensateur.
Très bien faites et très complètes.
À regarder plusieurs fois.
Energie
Quantité d'énergie stockée dans un condensateur
Comme il a été dit plus haut, un condensateur est un composant qui peut stocker de l'énergie.
On exploite cette propriété dans des applications comme par exemple l'éclairage de feux de fin de convois quand la voie n'est plus alimentée.
Formule de calcul :
E = 0,5·C·u²
E en joules
C en farads
u en volts (tension aux bornes du condensateur)
Exemples :
u (volts)
10
25
25
100
2,5
2,5
C
1 µF
1 000 µF
10 000 µF
47 nF
1 farad
500 farad
E
5 mJ
312 mJ
3,125 J
235 µJ
3,125 J
1562,5 J
millijoule
microjoule
On remarque qu'un condensateur de 1 farad chargé à 2,5 volts contient autant d'énergie qu'un condensateur de 10 000 µF chargé à 25 volts...
... mais le super-condensateur de 1 farad est beaucoup plus petit.
Pour donner un ordre d'idée, une balle de Winchester 243 possède une énergie de 2600 joules, et un super-condensateur de 500 farads en contient environ 1500 !
Impressionnant, non ?
Oui et non :
Oui, il faut être très prudent lorsqu'on manipule des super-condensateurs de forte capacité.
Non, ce n'est pas si énorme que cela. Les batteries Lithium au format LR6 emmagasinent une quantité d'énergie environ 10 à 20 fois supérieure, pour un volume et un poids équivalent. Nous allons le voir ci-dessous.
Équivalence joule ⇒ wattheure
En terme d'énergie nous sommes plus habitués à manier les wattheures ou les kilowattheures que les joules.
1 Wh = 3600 joules ⇒ 10 000 joules = 2,77778 Wh
Le super-condensateur de 500 farads ci-dessus contient donc 1562 joules, soit 0,434 Wh.
Pour mémoire, une batterie lithium de 1,5 volts et 5500 mAh contient 8,25 Wh.
u (volts)
10
25
25
100
2,5
2,5
C
1 µF
1 000 µF
10 000 µF
47 nF
1 farad
500 farad
E
5 mJ
312 mJ
3,125 J
235 µJ
3,125 J
1562,5 J
Wh
86 µWh
0,86 mWh
0,86 mWh
434 mWh
Les quantités d'énergie emmagasinées dans un condensateur sont finalement assez faibles, voir très faibles, sauf dans le cas des super-condensateurs de forte capacité.
Impédance
Impédance d'un condensateur
Un condensateur est un isolant vis à vis d'une tension continue, mais il présente une conduction lorsqu'il y a variation de tension à ses bornes.
Il est facile de comprendre que cette conduction est due à l'échange des charges entre les électrodes, lorsque le condensateur est soumis à une tension qui varie.
Il est tout aussi facile de comprendre que cette conduction augmentera avec la valeur capacitive et aussi avec la fréquence de la tension alternative.
En réalité, on caractérise plutôt l'inverse de la conduction. Il s'agit de l'impédance.
L'impédance caractérise l'opposition au passage du courant alternatif, au même titre que la résistance caractérise l'opposition au passage du courant.
Calcul de l'impédance :
Zc = 1 / C·2·π·f
(Le point «milieu de ligne» remplace le signe «x» )
Zc est exprimée en ohms (comme pour les résistances).
C est en farad
f est la fréquence exprimée en Hz (herz).
Le petit tableau ci-dessous donne quelques points de repères :
f (herz)
1 000
1 000
50
50
50
50
50
1 MHz
C
1 µF
10 µF
1 µF
10 µF
100 µF
1 000 µF
10 000 µF
220 nF
Zc (ohms)
160
16
3200
320
32
3,2
0,32
0,7
Dans ce tableau ne figurent pas d'exemples de calculs pour les super-condensateurs : ils ne sont pas adaptés au fonctionnement avec des tension alternatives.
Ce qu'on attend d'eux, c'est de stocker des quantités d'énergie importantes et de se rapprocher du fonctionnement des batteries.
Réservoir d'énergie
Le condensateur comme réservoir d'énergie
(Exemple des feux de fin de convoi)
L'application «feux de fin de convois» est détaillée dans la publication accessible ICI.
Ci-dessous, seul l'aspect «choix des condensateurs» est traité.
Le tableau répété ci-dessous montre clairement que seuls les condensateurs et super-condensateurs supérieurs à 100 µF ont une chance de pouvoir être utilisés comme réservoirs d'énergie pour, par exemple, alimenter une LED pendant un temps donné.
u (volts)
10
25
25
25
100
2,5
2,5
C
1 µF
100 µF
1 000 µF
10 000 µF
47 nF
1 farad
500 farad
E
5 mJ
31,2 mJ
312 mJ
3,125 J
235 µJ
3,125 J
1562,5 J
Wh
8,6 µWh
86 µWh
0,86 mWh
0,86 mWh
434 mWh
Principe de fonctionnement du circuit électronique proposé ci-dessous :
– la tension de voie est redressée (D1), filtrée (C2) puis régulée (L7805).
– cette tension régulée charge un super-condensateur de 1 farad à travers la diode D1.
– une fois chargé, le super-condensateur alimente les LED, même si la tension de voie n'est plus présente.
La diode D3 a un double rôle :
-
un super-condensateur est un élément fragile : une surcharge de quelques dixièmes de volts lui serait fatale.
La diode D3 provoque une chute de tension d'environ 0,7 volts ⇒ le condensateur se charge à seulement 4,3 volts. Ainsi on est certain que la tension ne viendra pas frôler la valeur de 5 volts, au delà de laquelle le super-condensateur est en danger. -
la diode D3 empêche le super-condensateur de se décharger dans le régulateur lorsque la tension de voie n'est plus présente.

Détermination de la durée d'alimentation des LED avec un condensateur de 1 farad.
Le but est de maintenir les LED allumées alors que la voie n'est plus alimentée.
Pour cette fonction, seuls les composants entourés en orange sont actifs :
-
D3 empêche la décharge du super-condensateur ailleurs que dans les LED ;
-
le super-condensateur se comporte en source d'énergie et se décharge dans les LED à travers les 2 résistances de 5600 Ω, R3 et R4 ;
Les essais ont été menés avec un super-condensateur de 1 farad : pas trop volumineux ; tension 5 volts.
La tension de charge initiale du super-condensateur est 4,3 volts.
La tension aux bornes d'une LED rouge traversée par un courant de 1 mA est d'environ 1,55 volt.
En dessous de 1,5 volt, aucun courant ne peut traverser la LED (presque).
⇒ donc, au cours de sa décharge, lorsque le condensateur n'est plus chargé qu'à ≈ 1,5 volt, il ne peut plus faire circuler de courant dans la LED.
Ce dernier point est important :
En effet, la courbe de décharge du condensateur ne tend pas vers 0 volt, mais vers ≈ 1,5 volt.
Cette tension de 1,5 volt représente donc la «tension plancher» du condensateur ⇒ c'est son «zéro volt» à lui.
On considère que ce plancher sera atteint au bout d'un temps de décharge égal à 5T, c'est-à-dire 5 fois la constante de temps (voir le chapitre «Constante de temps» ci-dessus), avec :
-
R = 5600 / 2 = 2800 Ω (2 résistances en parallèle)
-
C = 1 farad
⇒ durée de décharge = 5·R·C ≈ 5 x 1x 2800 ≈ 14 000 secondes (presque 4 heures).
En réalité il faut plutôt compter sur une durée de conduction de 3T à 4T.
En effet, à 5T, le courant qui traverse les LED est extrêmement faible.
⇒ les LED ne seront donc raisonnablement visibles que pendant environ 8400 à 11 000 secondes,
ce qui représente tout de même 2 h 30 à 3 heures.
Variations sur un même thème
Deux à trois heures de visibilité des LED c'est bien.
Peut-être que 10 minutes sont suffisantes.
Peut-être aussi qu'il n'est pas nécessaire que les LED éclairent autant.
Peut-être que si les LED utilisées sont très efficaces, la valeur des résistances R3 et R4 peut être augmentée.
Voici quelques calculs estimatifs rapides pour différents cas :
Durée souhaitée de visibilité des LED = 5 minutes, soit 300 secondes.
R3 = R4 = 5600 Ω
R = 5600 / 2 = 2800 Ω
On admet un temps de visibilité égal à 3T (3 fois la constante de temps)
⇒ 3T = 300 secondes
⇒ T = 100 s
⇒ C = T / R = 100 / 2800
⇒ C ≈ 0,036 farads, soit C ≈ 36 000 µF
Vu sur Aliexpress : un condensateur électrolytique de seulement 22 000 µF / 63 volts mesure 35 x 50 mm, c'est à dire quasiment la taille d'un super-condensateur de 500 farads !
C'est énorme !
⇒ Impossible à loger dans un wagon.
Conclusion : il faut choisir un super-condensateur de 0,1 farad / 5 volts (100 000 µF) qui se présente sous forme d'un disque de dimensions inférieures à 15 x 15 mm.
La durée de visibilité sera supérieure à 700 secondes.
Il faut cependant être prudent avec ces petits super-condensateurs : leurs courants de charge et de décharge sont limités à quelques dizaines de milliampères.
Durée souhaitée de visibilité des LED = 1 minute, soit 60 secondes.
Les LED sont de bonne qualité ⇒ R3 et R4 peuvent être augmentées à 12 kΩ
R = 12 000 / 2 = 6 000 Ω
On admet un temps de visibilité égal à 3T (3 fois la constante de temps)
⇒ 3T = 60 secondes
⇒ T = 20 s
⇒ C = T / R = 20 / 6 000
⇒ C ≈ 0,003 farads, soit C ≈ 3 000 µF
Valeur normalisée la plus proche : 3 300 µF / 6,6 V ⇒ dimensions : D = 10 mm ; L = 25 mm
Dans ce cas, un condensateur électrolytique classique convient parfaitement.
Il est facilement logeable dans un matériel roulant.
Un condensateur 3 000 µF / 6,3 V ne coûte que 0,40 €
Si le but est tout simplement de maintenir les feux de fin de convoi allumés, malgré des contacts imparfaits entre la voie et les roues...
R = 5 600 / 2 = 2 800 Ω
On admet un temps de visibilité égal à 3T (3 fois la constante de temps)
⇒ 3T = 1 secondes
⇒ T = 0,33 s
⇒ C = T / R = 0,33/ 2 800
⇒ C ≈ 0,003 farads, soit C ≈ 120 µF
Valeur normalisée la plus proche : 100 µF ou 220 µF
Un condensateur 220 µF / 50 V mesure 10 x 13 mm.
Très facile à loger dans un wagon.
Note :
Si vous n'avez pas dans vos tiroirs le condensateur de la valeur déterminée, choisissez-en dont la valeur est immédiatement supérieure. Le résultat n'en sera que meilleur.
Lissage
Le condensateur pour «lisser» une tension redressée
Voici à quoi ressemble la tension à la sortie d'un redresseur double alternance.

On a bien une tension positive, mais on ne peut pas l'appeler «tension continue».
En effet, elle est constituée d'une juxtaposition de demi-alternances de fréquence 100 Hz, c'est-à-dire le double de la fréquence de la tension du secteur.
L'adjonction d'un condensateur dit «de lissage» ou «de filtrage» permet de combler les creux et ainsi se rapprocher d'une tension continue.

Le mécanisme est simple :
-
pendant le flanc montant de la demi-alternance, le condensateur se charge ;
-
pendant le flanc descendant, il restitue une partie de l'énergie emmagasinée dans la charge (représentée ici sous forme d'une résistance).
Plus le condensateur a une forte capacité, plus le filtrage (lissage) sera efficace : courbe bleue.
L'allure de la courbe, bleue ou rouge, est en relation directe avec la fameuse constante de temps du condensateur.

Plus la capacité du condensateur est élevée, plus son temps de décharge dans la résistance de sortie est long, donc plus la décroissance est lente et meilleure est le «lissage» de la tension de sortie.
Ce lissage n'est pas parfait.
Il reste une «ondulation résiduelle».
Le problème qui se pose est donc le suivant : «Quelle est l'ondulation résiduelle acceptable ? »
La réponse dépend de plusieurs paramètres :
-
«quelle tension d'ondulation résiduelle la charge peut-elle accepter pour fonctionner correctement ? »
Si la charge est un amplificateur audio, même une faible ondulation résiduelle provoquera un ronflement audible. -
«le filtrage est-il suivi d'un étage de régulation dont le rôle est précisément de gommer cette ondulation ? »
Dans ce cas-là, on sera moins exigeant sur le lissage. Le régulateur permet de réaliser une économie sur le prix du condensateur, et un gain de place. -
«la charge est-elle variable, et dans quelle proportion ? »
Le filtrage devra être calculé pour convenir à la plus forte consommation de sortie. -
...
Une formule extrêmement simple permet de calculer la capacité du condensateur en fonction de l'ondulation résiduelle souhaitée :
C = I / (u·f)
C = courant de sortie en ampères
u = ondulation résiduelle en volts
f = fréquence de la tension redressée en herz
Premier exemple :
-
l'alimentation doit fournir 0,5 A en sortie, avec une ondulation résiduelle maximale de 5 volts ;
-
le primaire du transformateur est relié au secteur, dont la fréquence est 50 Hz.
⇒ fréquence de la tension redressée = 2 x 50 = 100 Hz
⇒ C = 0,5 / (5 x 100)
⇒ C = 1000 µF
Deuxième exemple :
-
l'alimentation doit fournir 0,5 A en sortie, avec une ondulation résiduelle maximale de 2 volts ;
-
le primaire du transformateur est relié au secteur, dont la fréquence est 50 Hz.
⇒ fréquence de la tension redressée = 2 x 50 = 100 Hz
⇒ C = 0,5 / (2 x 100)
⇒ C = 2500 µF
Troisième exemple :
-
l'alimentation doit fournir 2 A en sortie, avec une ondulation résiduelle maximale de 0,5 volts ;
(Ce serait par exemple l'exigence pour une alimentation 5 V / 2 A destinée à alimenter un montage électronique). -
le primaire du transformateur est relié au secteur, dont la fréquence est 50 Hz.
⇒ fréquence de la tension redressée = 2 x 50 = 100 Hz
⇒ C = 2 / (0,5 x 100)
⇒ C = 40 000 µF
C'est un condensateur énorme ! (et cher).
Dans ce cas-là :
-
soit on admet une ondulation beaucoup plus importante pour diminuer la taille du condensateur, et on fait suivre le filtrage par un circuit intégré régulateur ;
-
soit on utilise la technique du «découpage» qui va produire une alimentation primaire à fréquence élevée (> 50 kHz) et ainsi permettre de diminuer la taille des condensateurs.
Par exemple, avec une fréquence de découpage de 100 kHz, un courant de sortie de 2 A et une ondulation résiduelle maximale de 0,2 volts, il suffirait d'un condensateur de 100 µF sur la tension de sortie.
Temporisateur
Le condensateur comme temporisateur
Cette utilisation du condensateur découle directement de la notion de «constante de temps».

Lorsque le condensateur se charge à travers une résistance, la tension à ses bornes augmente progressivement.
Un niveau de tension donné correspond donc à une durée.
Il suffit de détecter ce niveau de tension.

Premier montage ultra-simple : principe
-
au départ, le condensateur C est déchargé. Le courant «Ib» est donc nul et le transistor ne conduit pas.
⇒le relais n'est pas activé. -
on actionne brièvement le poussoir ⇒ C se charge instantanément à la tension d'alimentation, à travers la diode. (NDLR : j'aurais préféré une 1N4001, plus costaude)
-
C commence à se décharger à travers la résistance R et la jonction «base-émetteur» du transistor.
⇒ la jonction «collecteur-émetteur» du transistor est conductrice. Le relais est actionné.
Le transistor fonctionne comme un interrupteur. -
tant que le courant Ib est suffisant, le transistor conduit et le relais reste actionné.
-
lorsque le condensateur est suffisamment déchargé, le transistor cesse d'être conducteur et le relais retombe à sa position de repos.
Conditions de départ :
– supposons que la tension d'alimentation est 6 volts.
– supposons que le condensateur a une capacité de 4700 µF.
– typiquement, la résistance de la bobine d'un relais de 6 volts est d'environ 80 Ω à 100 Ω.
⇒ la valeur de la résistance R doit être 15 à 10 fois plus élevée, soit 1200 Ω à 800 Ω, pour être certain que le transistor se comporte comme un interrupteur vis-à-vis du relais : fonctionnement «à saturation».
Choisissons R = 1kΩ.
– le transistor cesse de conduire lorsque sa tension «base-émetteur» passe en-dessous de 0,7 volt.
Calcul sommaire (très sommaire)
À partir du moment où le condensateur n'est plus chargé qu'à ≈ 0,7 volts, il arrête quasiment de se décharger.
Ce dernier point est important :
En effet, la courbe de décharge du condensateur ne tend pas vers 0 volt, mais vers ≈ 0,7 volt.
Cette tension de 0,7 volt représente donc la «tension plancher» du condensateur ⇒ c'est son «zéro volt» à lui.
⇒ on considère que ce plancher sera atteint au bout d'un temps de décharge égal à 5T, c'est-à-dire 5 fois la constante de temps (voir le chapitre «Constante de temps» ci-dessus).
⇒ durée de conduction = 5·R·C ≈ 5 x 1000 x (4700/1 000 000) ≈ 23,5 secondes
En réalité, avec ces valeurs de R et de C, on obtient des durées de temporisations de l'ordre de 18 à 25 secondes.
Cela dépend de la sensibilité du relais et de la tension de seuil exacte de la jonction «base-émetteur» du transistor.
Cela dépend aussi de la tolérance sur la valeur de la capacité.
Un tel schéma est très simple et fonctionne parfaitement bien, mais l'obtention d'une temporisation précise nécessite d'ajuster la valeur de la résistance R associée au condensateur choisi.
Quelques durées de temporisations précalculées :
Plus sérieux : temporisateur avec un NE555
Tension relais
(V)
5
5
5
5
5
5
12
12
12
Résistance bobine relais
(Ω)
≈ 45
≈ 45
≈ 45
≈ 45
≈ 45
≈ 45
≈240
≈ 240
≈ 240
Résistance R
(Ω)
680
680
680
680
680
680
2200
2200
2200
Capacité
(µF)
100
220
470
1000
4700
1 farad
220
4700
1 farad
Temporisation
(s)
0,34
0,75
1,6
3,4
16
3400
2,4
52
11 000
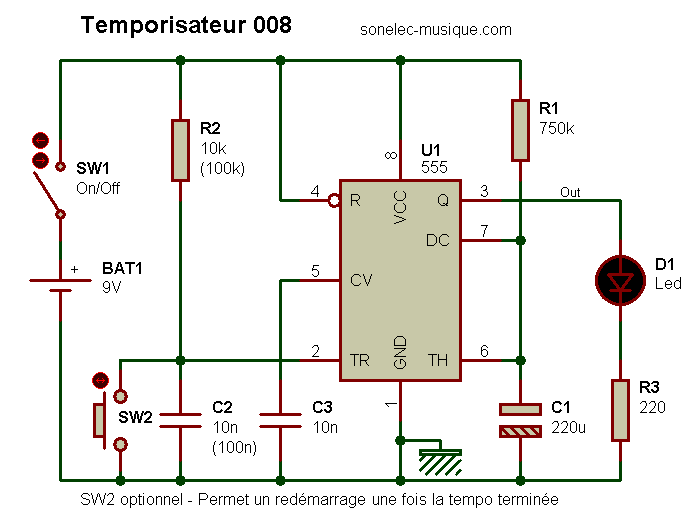
Ce schéma est issu du site de SONELEC :
https://www.sonelec-musique.com/electronique_realisations_temporisateur_008.html
Une fois la tension d'alimentation établie, le poussoir SW2 permet de déclencher la temporisation.
Les deux composants R1 et C1 déterminent a durée de la temporisation suivant la relation T = R1·C1·1,1
-
T en secondes ;
-
R1 en ohms ;
-
C1 en farads
Quelques exemples :
Résistance R1
(Ω)
1000
10 000
100 000
2200
330 000
10 000
100 000
Capacité C1
(µF)
100
220
220
1000
100
1 farad
1 farad
Temporisation
(s)
0,11
2,42
24,2
2,42
36
11 000
(≈ 3 heures)
30 heures
Un constat évident : le NE555 offre une bien plus grande souplesse et une bien meilleure précision :
-
une même durée peut être obtenue avec des couples [R1-C1] très différents sans que cela pose de problème de fonctionnement ;
-
les gammes de valeurs pour R1 et C1 sont très étendues : 100 Ω à 1 MΩ pour R1 et ≈ 1µF à plusieurs farads pour C1 ;
-
la commutation de la tension de sortie est rapide et franche, ce qui n'est pas le cas du temporisateur à transistor ci-dessus ;
-
si on remplace R2 par un potentiomètre de 100 kΩ, on réalise une temporisation ajustable.
Le NE555 est un circuit intégré aux possibilités multiples :
-
temporisateur ;
-
impulsion unique ;
-
oscillateur ;
-
générateur PWM ;
-
etc.
⇒ dans tous les cas, un condensateur servira à générer la base de temps.
Oscillateur
Le condensateur comme élément d'oscillateur
Voici le schéma d'un oscillateur de type «R·C» ultra simple :
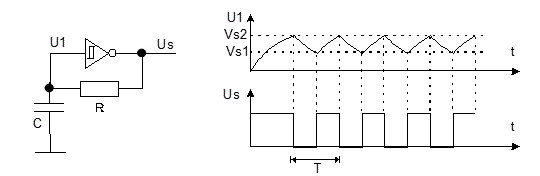
Comme d'habitude, le fonctionnement est basé sur la charge et la décharge d'un condensateur.
Dans ce schéma, l'élément actif est un circuit intégré inverseur qui a 2 tensions de seuils de basculement.
En jouant avec ces 2 seuils le montage génère en sortie une tension carrée (non sinusoïdale), exactement comme le fait le NE555.
Il existe des quantités de types d'oscillateurs.
On trouve de très nombreux schémas sur le net.
Le but n'est pas de les étudier ici.
Simplement il faut retenir que les fréquences d'oscillations vont de quelques hertz à plusieurs mégaherz (et même plus), et que dans tous les cas un ou plusieurs condensateurs participent à la génération des oscillations.
Antiparasite
Le condensateur comme antiparasite
Voici le schéma d'une alimentation régulée, basée sur un circuit intégré 7805 (5 volts).
Antiparasitage d'un régulateur de tension

On remarque 2 condensateurs en parallèle sur l'entrée du 7805 :
-
un condensateur 1000 µF ;
-
un condensateur 220 nF.
Curieux, non ?
Le condensateur de 220 nF a une capacité environ 5000 fois plus faible que celle de son voisin. Que fait-il là ?
En sortie du 7805 il y a aussi un condensateur de 100 nF.
Explications
Dans le chapitre «Le condensateur utilisé pour lisser une tension redressée», on a vu que la tension en sortie du redresseur est positive mais non continue.
Pour pouvoir fonctionner, le 7805 a besoin d'une tension proche d'une tension continue, c'est-à-dire «pas trop perturbée».
⇒ le rôle du condensateur de 1000 µF est de «lisser» cette tension.
Mais il n'est pas excellent pour réagir à des fréquences élevées.
Les deux condensateurs (non polarisés) de 220 et 100 nF, eux, «appartiennent» à l'environnement du 7805.
Cette disposition des condensateurs est une recommandation de la datasheet du 7805 (recommandation «constructeur»).
Dans le chapitre «Impédance d'un condensateur», on a vu comment calculer l'impédance d'un condensateur.
Zc = 1 / C·2·π·f
Plus la fréquence est élevé, plus cette impédance est faible, c'est-à-dire moins le condensateur oppose de résistance au passage d'un courant alternatif.
Cette propriété est mise à profit pour «détourner» vers la masse les perturbations (les parasites) présentes en sortie de la partie redressement-filtrage.
Que sont ces parasites ?
Ce sont des perturbations électriques et électromagnétiques qui viennent se superposer à la tension filtrée.
Elles sont générées par les tubes fluorescents, par les collecteurs des moteurs, des fermetures et ouvertures de contacts, etc.
Elles arrivent soit par les fils électriques (secteur, câblages), soit elles sont captées par ces même fils qui se comportent comme des antennes réceptrices.
Ces perturbations ont des fréquences équivalentes élevées : de 20 kHZ à plusieurs mégahertz.
Prenons le cas d'un condensateur de 220 nF.
Son impédance vis à vis d'une perturbation de fréquence 1 MHz est Zc = 1 / (100/10^9 x 2 x π x 100 000)
⇒ Zc ≈ 0,7 Ω
Autrement dit, vis à vis de la perturbation, le condensateur de 220 nF se comporte presque comme un court-circuit : il dérive la perturbation vers la masse.
⇒ le rôle de ces deux condensateurs (220 nF et 100 nF) est donc de bloquer les parasites pour éviter de perturber le fonctionnement du 7805.
Le condensateur de 100 nF a pour rôle d'achever le travail du condensateur de 220 nF : il court-circuite vers la masse le reliquat des perturbations qui auraient éventuellement traversé le 7805.
Il a une impédance Zc = 1,6 Ω à 1 MHz.
Ces condensateurs sont de technologie polycarbonate, polyester, polypropylène, polystyrène..., famille de condensateurs qu'on range dans la catégorie «à diélectrique plastique».
Ils se comportent remarquablement bien en fréquence (Ils sont employés jusqu'à des fréquences de 10 GHz).
Remarque :
Plus la perturbation est de fréquence élevée, meilleure est son atténuation par ces 2 condensateurs.
On a vu qu'un condensateur est un conducteur en alternatif.
Ici, on lui demande de se comporter comme un presque-court-circuit vis à vis des parasites.
Limiteur
Antiparasitage d'un petit moteur
On voit souvent ce type de branchement à l'arrière de petits moteurs.

Un condensateur de 100 à 400 nF est connecté entre les bornes du moteur.
Il court-circuite les parasites créés par le collecteur.
Deux autres condensateurs de 47 à 220 nF sont connectés entre la carcasse métallique du moteur et les bornes d'alimentation.
Ils dérivent le restant des parasites vers la carcasse, évitant qu'ils soient ainsi émis sous forme de rayonnement électromagnétique vers l'extérieur du moteur par les fils d'alimentation.
Les condensateurs utilisés sont en technologie «plastique» ou «céramique», ou mixte, comme dans le cas présent.
Note :
Les petits condensateurs ci-dessus marqués «473» sont des condensateurs céramiques.
Le marquage «473» correspond à 47 000... picofarads, soit 47 nF. (voir le chapitre «Marquage et lecture » ).
Le condensateur comme limiteur de courant
En courant alternatif, un condensateur présente une impédance Zc = 1 / C·2·π·f
Copie du petit tableau récapitulatif figurant dans le chapitre «L'impédance d'un condensateur» :
f (herz)
1 000
1 000
50
50
50
50
50
1 MHz
C
1 µF
10 µF
1 µF
10 µF
100 µF
1 000 µF
10 000 µF
220 nF
Zc (ohms)
160
16
3200
320
32
3,2
0,32
0,7
Supposons qu'on désire alimenter une LED avec une tension alternative.
Le schéma qui vient tout naturellement à l'esprit est le suivant :
Pendant l'autre demi-alternance, c'est la diode de protection D2 qui est traversée par le courant de 20 mA.
En réalité, le courant dans la diode D2 est un peu supérieur à 20 mA, du fait de sa tension aux bornes de l'ordre de 0,7 V, alors que la tension aux bornes de la LED est de l'ordre de 2 volts.
La puissance dissipée par la résistance R1 vaut P = U·I
U = 10 volts (12 volts de l'alimentation, moins 2 volts de la tension aux bornes de la LED)
I = 20 mA
⇒ P = 10 x 0,020
⇒ P = 200 mW
Une résistance 1/4 W peut convenir, mais c'est un peu juste, si le montage est logé dans une petit volume non ventilé.
On constate que ce montage est parfaitement valable, mais uniquement si la tension alternative est de l'ordre de 12 V maxi.
Pour s'en convaincre, voici le calcul pour une tension de 24 volts AC :
U = 22 volts (24 volts de l'alimentation, moins 2 volts de la tension aux bornes de la LED)
I = 20 mA
⇒ puissance dissipée par la résistance R1 : P = 22 x 0,020 ⇒ P = 440mW
⇒ il faut prévoir un modèle qui peut dissiper 1W (pour les mêmes raisons que ci-dessus).
⇒ valeur de la résistance R1 : R1 = 22 / 0,020 = 1 100 Ω
Au passage, on remarque que la LED, qui n'éclaire qu'une alternance sur deux, ne dissipe que
P = 2 x 0,020 / 2 = 20 mW, soit 22 fois moins que la résistance de limitation !
Quel gaspillage dans la résistance !
Et si au lieu de «résistance» on parlait «impédance» ?
Puisque le montage fonctionne en courant alternatif, il suffit de remplacer la résistance R1 par une impédance.
Question : quelle est la valeur d'un condensateur d'impédance 510 Ω à la fréquence de 50 Hz ?
Zc = 1 / (C x 2 x π x f) ⇒ C = 1 / Zc·2·π·f
C = 1 / (510 x 2 x 3,14 x 50)
C = 6,24 µF
⇒ avec une tension alternative de 12 V / 50 Hz, un condensateur de 6 µF / 25 V aurait le même effet qu'une résistance de 510 Ω. (2 condensateurs de 3,3 µF en parallèle).
Attention ! ces condensateurs ne doivent pas être polarisés. Or, des condensateurs de 3,3 µF / 63 V en technologie «plastique» sont TRES volumineux !
Le petit tableau ci-dessous donne, pour différentes tensions alternatives à 50 Hz, quelques valeurs du condensateur qui remplace la résistance R1, en limitant le courant à 20 mA :

R1 limite le courant dans la LED ;
D2 protège la LED lors de la demi-alternance négative.
Avec R1 = 510 Ω et V = 12 V AC, le courant dans la résistance s'établit à environ 20 mA.
⇒ D1 (LED) voit donc passer un courant de ≈ 20 mA, mais seulement une demi-alternance sur deux.
Tension AC (volts)
12
24
48
240
C
(µF ou nF)
6,24 µF
2,9 µF
1,4 µF
270 nF
Zc
(ohms)
510
1 100
2 300
12 000
Pour les tensions jusqu'à 100 V AC, on constate que la limitation de courant de la LED nécessite des condensateurs de valeur supérieure à 1µF.
Les modèles non polarisés, dans ces valeurs, sont encombrants et chers.
Ci-dessous, voici 2 schémas pratiques utilisant un condensateur comme limiteur d'intensité :

Le deuxième circuit utilise deux LED tête-bêche.
L'une éclaire pendant que l'autre est éteinte et vice versa.
On évite ainsi un papillotement de l'éclairage et l'intensité lumineuse est doublée.
Les résistances R1 et R2 sont destinées à atténuer le choc de courant si la mise sous tension a lieu à l'instant précis du sommet d'une alternance.
R1 et R2 seront calibrées entre 47 Ω et 100 Ω.
Le tableau ci-dessous donne quelques exemples pour différents courants dans les LED, différentes valeurs et fréquences de la tension V AC.
Tension AC (volts)
5
5
5
5
5
12
12
12
12
240
240
240
240
f
(Hz)
50 Hz
50 Hz
50 Hz
1 000 Hz
10 000 Hz
50 Hz
50 Hz
50 Hz
1 000 Hz
50 Hz
50 Hz
50 Hz
50 Hz
I led
(mA)
2 mA
5 mA
10 mA
20 mA
20 mA
2 mA
5 mA
10 mA
20 mA
2 mA
20 mA
100 mA
500 mA
Zc
(ohms)
1 500 Ω
600 Ω
300 Ω
150 Ω
150 Ω
5 000 Ω
2 000 Ω
1 000 Ω
500 Ω
120 kΩ
12 kΩ
2 400 Ω
480 Ω
C
(µF ou nF)
2 µF
5,3 µF
10 µF
1 µF
100 nF
640 nF
1,6 µF
3,3 µF
320 nF
27 nF
270 nF
1,3 µF
6,7 µF
C
(µF ou nF)
Existe en non polarisé
Existe en non polarisé
Existe en non polarisé
Existe en non polarisé
Existe en non polarisé
LED de puissance
Plus la fréquence est élevée et plus le courant est faible, plus il est facile de trouver un condensateur «plastique» qui convient.
On trouve des condensateurs électrolytiques non polarisés.
En fait, ce sont 2 condensateurs électrolytiques, montés tête-bêche en série.
Ils sont destinés à des applications «audio», et donc leur tension de service dépasse rarement 100 volts.
On voit aussi que si on cherche à alimenter sur ce principe des LED de puissance (1 à 3 watts) à partir du secteur, on aura du mal à trouver un condensateur adapté, avec une tension de service de 400 volts.
... et la puissance dissipée par le condensateur ?
On a vu précédemment que si on utilise une résistance de limitation, on est vite limité par sa dissipation thermique.
Avec un condensateur on n'a pas ce problème.
Un condensateur est une résistance en alternatif (impédance), mais comme le courant qui le traverse sert à sa charge et décharge (et non pas à de l'effet Joule), le condensateur ne chauffe pas.

Associations de condensateurs
Association en parallèle
-
les capacités s'ajoutent : C = C1 + C2 ;
-
la tension de service du groupe est la tension de service la plus faible des deux.
Association
Remarque :
Dans un montage comme celui-ci, la mise en parallèle des condensateurs n'a pas pour but d'augmenter la capacité totale.

Chaque condensateur a un rôle différent :
-
1000 µF pour filtrer la tension redressée ;
-
220 nF pour court-circuiter les parasites vers la masse.
Association en série
-
la capacité résultante C se calcule ainsi : 1/C = 1/C1 + 1/C2 + ... + 1/Cn
-
les tensions de service s'ajoutent.
Pour faire simple : 2 condensateurs de 1000 µF / 25 V en série forment un condensateur de 500 µF avec une tension de service de 50 volts.
Cette disposition est utilisée en particulier avec les super-condensateurs :
Un super-condensateur simple a une tension de service de 2,7 volts ;
⇒ en associant 2 super-condensateurs de 2 farads en série, on obtient un condensateur de 1 farad avec une tension de service de 5,4 volts, bien adapté à une utilisation avec des montages alimentés sous 5 volts.
Association en série, tête-bêche, de 2 condensateurs électrolytiques
Lorsqu'on a besoin d'une forte capacité non polarisée, une solution consiste à monter deux condensateurs électrolytiques en série, tête-bêche, et de les encapsuler dans un même boîtier.

Lorsque la tension s'inverse, un des condensateurs est polarisé dans le bon sens, et l'autre en inverse.
Celui qui est polarisé en inverse laisse passer le courant, sans être détruit.
(Le mécanisme électro-chimique est complexe et nous ne l'expliquerons pas ici).
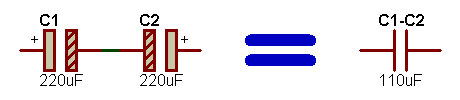
Ce type de montage est par exemple utilisé en audio :
Pour éviter que le HP aigu soit soumis aux fréquences basses – pour lesquelles il n'est pas du tout conçu et qu'il est bien incapable de transmettre – on lui adjoint en série un condensateur dont l'impédance doit être forte pour les fréquences basses, et faibles pour les fréquences aigues.
Le condensateur est très bien adapté à cet usage puisque son impédance diminue avec l'augmentation de la fréquence.
Cependant le calcul montre qu'on a besoin d'une capacité de 2 à 8 µF (suivant le type de HP).
Pour obtenir un condensateur non polarisé de 5 µF (par exemple), on associe 2 condensateurs de 10 µF, montés en série, tête-bêche.


That's all Folks !
Gros topo sur les condensateurs
bottom of page




_p.png)