Difficile de faire plus simple : une seule pièce d'habitation et un toit plat.
Dimensions extérieures : environ 45 x 54 x 33 mm.
Quatre ouvertures dont une porte.
... et c'est tout.
Plus modeste, on peut pas.
Les murs ont une épaisseur de 3 mm.


Difficile de faire plus simple : une seule pièce d'habitation et un toit plat.
Dimensions extérieures : environ 45 x 54 x 33 mm.
Quatre ouvertures dont une porte.
... et c'est tout.
Plus modeste, on peut pas.
Les murs ont une épaisseur de 3 mm.
Pour imprimer cette petite maison j'ai choisi du fil PolyWood. C'est un PLA avec du bois qui donne à la pièce un aspect "bois mat" ou "terre sèche". Facile à enduire et à peindre.
Suivant l'imprimante utilisée, il sera nécessaire de réduire au papier de verre les dimensions du toit pour qu'il s'encastre correctement et vienne en appui sur les petites nervures qui ceinturent le bâtiment à l'intérieur des murs.
Pour éviter l'affaissement des linteaux l'impression est paramétrée avec "supports d'impression", c'est à dire que les porte et fenêtres (ben oui, ya qu'une porte ! ) seront remplies d'une sorte de nid d'abeille qui supportera les linteaux au moment de leur impression.
Il faudra ensuite désoperculer toutes les ouvertures pour les débarrasser de ces supports, puis ébavurer correctement.

La maison, avec son toit, et la porte partiellement désoperculée.
Note :
Cette petite maison peut être facilement imprimée à l'échelle "N".
Il suffit, dans CURA by Dagoma, d'utiliser les mêmes fichiers ".stl" et d'appliquer le coefficient de réduction 0,54. (Hé oui ! Pas besoin de redessiner).
L'impression prendra 20 minutes et 4 grammes de PLA pour un coût matière de l'ordre de 0,20€ !
Si l'échelle 1:43 vous tente, il suffit d'appliquer un coefficient x2 dans CURA.
Il faudra 5 heures d'impression et 73 grammes de PLA (moins de 4€).
C'est encore jouable.
Ah ! petite remarque : le bâtiment est marqué "HUGO 2017" à l'intérieur.
Mon petit fils voulait que "son œuvre" soit signée ! (c'est la seule chose que j'ai faite sur ce modèle).
Téléchargements :

Petite maison en adobe
Un de mes petits fils voulait absolument dessiner et imprimer une maison en 3D.
J'ai orienté son choix vers un modèle simple : une petite maison de paysan modeste de la région de Santa Fe, en adobe, qui va me servir sur mon réseau. Tant qu'à faire...
ÉLECTRONIQUE de BASE
Du pico au giga :
les puissances de 10
Mis à jour le 10/04/2022
Je devrais plutôt titrer : "du yocto au yotta".
Note :
Ce «yotta»-là n'a rien à voir avec le "iota", 9e lettre de l'alphabet grec.
En français, la lettre iota est utilisée pour décrire une petite quantité négligeable. L'expression «pas un iota», c'est-à-dire «pas la plus petite quantité» fait référence à une phrase du Nouveau Testament (Matthieu 5:18) : «tant que le ciel et la terre ne passeront pas, il ne disparaîtra pas de la loi un seul iota ou un seul trait de lettre».
(Petite phrase piquée dans Wikipedia. On s'amuse comme on peut...).
Le présent "topo" propose de comprendre l'écriture des nombres en utilisant les puissances de 10.
Pas de panique !
Il ne s'agit pas de subir un cours de maths trapu, mais seulement d'acquérir les notions indispensables pour manipuler les valeurs de nos composants électroniques, FACILEMENT et sans erreur de calcul.
Préambule :
-
1, 2, 3, ... , 9 et 0 sont des chiffres. Il y a donc dix chiffres au total, pas un de plus.
-
123 ; 24 ; 0,7 ; 125 467 543 321 sont de nombres.
Les nombres sont composés de plusieurs chiffres et ils sont en quantité infinie.
... et voilà où commencent les difficultés :
Comment énoncer ce fameux nombre «125 467 543 321» ci-dessus ?
Et encore, je l'ai écrit en séparant en tranches de 3 chiffres.
S'il est écrit ainsi : «125467543321», il devient quasi indéchiffrable.
... au fait, ce nombre s'énonce : 125 milliards 467 millions 543 mille 321
Pire !
Et celui-ci : 654858264475213524765 ?
Oui, moi aussi je sèche.
En utilisant les dénominations officielles :
654 trillions 858 billiards 264 billions 474 milliards 213 millions 624 mille 765 !!!
Une petite dernière
(juste pour finir de vous convaincre d'utiliser les puissances de 10) :
Quelle est la masse de la Terre ?
Environ 6 000 000 000 000 000 000 000 000 kg, soit 6 mille quadrillions de kilogrammes.
Bon, j'arrête ici.
Tout ceci montre à l'évidence que ce système d'écriture et de formulation des grands nombres (mais aussi des très petits) n'est pas efficace et qu'il faut imaginer autre chose.
Une remarque intéressante concernant la masse de la Terre : il est écrit «Environ...»
Ben oui, quel intérêt de connaître cette masse au kilogramme près ?
... ou même à la tonne près ?
... ou même à mille milliards de tonnes près ?
Il en sera de même pour toutes les grandeurs électroniques que nous serons amenés à manipuler :
-
des écritures à plus de 2 chiffres significatifs n'ont pas de sens pour des valeurs à 5% près ;
-
une écriture à 4 chiffres significatifs est suffisante pour des valeurs à 1 pour mille près.
Alors pourquoi traîner des chiffres qui donnent une illusion de précision, mais qui en réalité n'apportent que de la confusion ?
Supposons, pour vous en convaincre, que le calcul de la valeur d'une résistance nous donne comme résultat :
13 543 245 ohms, soit 13, 543 245 millions d'ohms.
La résistance de 13 543 245 ohms n'existe pas et n'existera jamais.
Nous savons que dans la série E12, la valeur la plus proche sera 12 millions d'ohms soit 12 000 000 d'ohms, à 5% près.
On a rarement besoin d'une précision supérieure, et même si ce choix semble n'être qu'un compromis, c'est notre seul choix et il est raisonnable.
Exemple de calcul en écriture strictement décimale
-
la résistance vaut 12000000 ohms
-
elle est traversée par un courant de 0,000002 ampères (A)
-
quelle est la tension aux bornes de la résistance ?
On applique la loi d'Ohm : U=R x I :
U = 12000000 x 0,000002
U = ?
IMBUVABLE !!!
Exprimées sous cette forme, on a aussi beaucoup de difficultés à énoncer les nombres :
-
12 000 000 se prononce «douze millions» ;
-
0,000002 se prononce... «deux millionièmes» ;
-
0,00003 se prononcerait «trois centmillièmes».
Pire encore : on n'a aucune idée de l'ordre de grandeur des valeurs manipulées.
En conclusion, cette notation, bien que parfaitement exacte :
-
ne nous « parle » pas ;
-
nous oblige à manipuler des nombres avec énormément de chiffres, au risque d'en perdre en cours de calculs ;
-
ne permet pas d'énoncer simplement les nombres en question.
De ce qui précède est née l'idée et l'absolue nécessité d'une écriture mathématique des nombres plus simple et plus efficace.
Introduction aux puissances de 10 :
Prenons comme exemple la valeur de résistance 1234 ohms. Elle peut s'exprimer de plusieurs façons, dans trois modes équivalents :
_p.png)
Ces écritures sont toutes exactes et parfaitement équivalentes.
Alors, laquelle choisir ?
Trois façons possibles d'écrire un nombre en puissances de 10 :
Préambule : écriture décimale
Le nombre est écrit en entier, sans multiplicateur.
Exemples :
-
140 000 000
-
0,023
Remarque : dans cet article, pour écrire des puissances de 10, on utilisera (faute de mieux) la notation «calculatrice» ou «en ligne» : «10^».
En effet, beaucoup de calculatrices ne disposent pas de l'affichage des indices et des exposants sous forme de petits caractères déportés en bas ou en haut.
... pas plus que l'éditeur qui sert à composer la page que vous lisez en ce moment. Dommage.
Exemple :
1,4x10^3
... qui se lit «1 virgule 4 ... 10 puissance 3» ou «1 virgule 4 ... 10 exposant 3»
Écriture mathématique :
Exemples :
-
14x10^7
-
0,140x10^9
-
1400x10^5 Ces 3 écritures sont rigoureusement équivalentes.
-
0,23x10^-1
-
230x10^-4 Ces 2 écritures sont rigoureusement équivalentes.
-
le nombre avant la puissance de 10 peut être plus petit que 1 ou plus grand que 1 ;
-
toutes les puissances de dix peuvent être utilisées.
Écriture scientifique :
-
1,4.10^8
-
2,3.10^-2
-
le nombre décimal devant la puissance de 10 est strictement compris entre 1 et 10, 10 non compris ;
-
l'exposant de 10 peut prendre toutes les valeurs, positives ou négatives nécessaires.
Écriture «ingénieur» :
L’écriture ingénieur est une écriture simplifiée des grands nombres, dérivée de l'écriture scientifique.
Cette écriture doit satisfaire deux conditions particulières :
-
l’exposant de « 10 » est un nombre entier multiple de 3, positif ou négatif ;
-
⇒ le nombre devant la puissance de 10 est donc obligatoirement un nombre décimal toujours compris entre 1 et 1000, 1000 non compris.
Exemples :
-
2,3.10^-3 ampères pour «2,3 milliampères» ;
-
42.10^6 ohms pour «42 mégohms».
-
une résistance de 470 000 ohms sera exprimée : 470.10^3 ohms.
-
une résistance 10 fois plus grande, soit 4 700 000 ohms sera exprimée : 4,7.10^6 ohms
(et non pas 4700.10^3 ohms).
Note : cette écriture basée sur les puissances de 10 multiples de 3 découle tout simplement de la façon d'écrire les nombres décimaux – qu'ils soient plus grands ou plus petits que 1 – en séparant les chiffres par tranches de 3 à partir de la droite.
Puissances de 10 et nombre de zéros :
Examinons les trois écritures équivalentes ci-dessous :
-
470 000 ohms (écriture décimale) ;
-
470 x 1000 ohms (écriture avec multiplicateur) ;
-
470.10^3 ohms (écriture "ingénieur").
Il apparaît donc que l'exposant de la puissance de 10 qui suit "470" correspond au nombre de zéros du multiplicateur, ou au nombre de zéros qu'il faut rajouter à "470" pour retrouver l'écriture décimale du nombre :
-
3 zéros dans le multiplicateur 1000 ⇒ 3 zéros à rajouter derrière 470 pour obtenir 470 000 ;
-
10^3 : puissance de 10 avec exposant 3 ⇒ 3 zéros à rajouter derrière 470 pour obtenir 470 000.
Ce n'est pas plus compliqué que cela !
... et pour les nombres plus petits que 1 ?
Examinons les trois écritures équivalentes ci-dessous :
-
0,000 047 farad (écriture décimale)
-
47 / 1 000 000 farad (écriture avec diviseur)
-
47.10^-6 farad (écriture "ingénieur").
Il apparaît donc que l'exposant de la puissance de 10 qui suit "47" correspond au nombre de zéros du diviseur (mais avec un signe "moins"), ou au nombre de pas dont il faut déplacer la virgule vers la gauche pour obtenir une écriture décimale du nombre :
-
6 zéros dans le diviseur 1 000 000 ⇒ 6 pas à gauche pour obtenir « 0,000 047 ».
-
10^-6, puissance de 10 avec exposant « - 6 » ⇒ 6 pas à gauche pour obtenir « 0,000 047 ».
Les puissances de 10 et leurs noms :
Dans l'expression orale il est tout de même assez pénible de prononcer les nombres ci-dessous tels qu'ils sont écrits :
-
470.10^3 ohms = quatre cent soixante dix, dix puissance trois ohms
-
47.10^-6 farad = quarante sept dix puissance moins six farad
C'est bien ainsi qu'on prononce les nombres en langage mathématique.
Mais pas dans le domaine technique.
On a donc attribué des noms et des symboles (ou préfixes) à ces puissances de dix.
⇒ l'expression et l'écriture sont plus compactes et un peu plus parlantes :
-
quatre cent soixante dix kiloohms
-
quarante sept microfarads
Voici un tableau, du yotta au yocto, qui donne ces noms :
On notera que les symboles des puissances au dessus de «3» sont en majuscules, et ceux des puissances inférieures à «0» sont en minuscules.
Eh oui. «kilo» fait exception en tant que puissance de 10 multiple de 3.
On notera aussi que 10^0 ne figure pas dans le tableau. En effet, 10^0 = 1 ⇒ Il n'y a pas besoin d'affecter un nom de multiplicateur à l'«unité».
«déca» est le seul symbole à 2 lettres, pour ne pas le confondre avec «déci».
_p.png)
Au delà de ce tableau, vers les exposants très élevés, on trouve le gogol (eh oui, ça ne s'invente pas) qui vaut 10^100 et qui a donné le nom de "google". Très forts les mecs ! (voir ICI).
Vous remarquerez quatre exceptions dans ce tableau : quatre puissances de 10 ne sont pas
des multiples de 3.
Il s'agit du déca (10^1) , de l'hecto (10^2), du déci (10^-1) et du centi (10^-2).
Ces quatre préfixes ne sont pas utilisés en électronique, mais ils sont encore très utilisés par les géomètres et les vignerons.
Rassurez-vous, il n'est pas utile de connaître tous ces préfixes et leurs symboles.
En effet, dans l'usage courant pour nos applications électroniques :
-
les valeurs de résistances s'échelonnent du milliohm au mégohm, càd 1x10^-3 à ≈100x10^+6 ;
-
les valeurs de capacités s'échelonnent du picofarad à quelques farads, càd 1x10^-12 à ≈ 500 ;
-
les valeurs d'inductances s'échelonnent du microhenry à quelques henrys, càd 1x10^-6 à ≈ 100 ;
-
les valeurs de courants s'échelonnent du microampère (parfois le nanoampère - 10^-9) à quelques ampères ;
-
les valeurs de tensions s'échelonnent du millivolt à quelques dizaines de volts ;
-
les valeurs de puissances (thermiques) s'échelonnent du milliwatt à quelques dizaines de watts.
En fait, en tant qu'amateurs électroniciens nous n'utiliserons que les préfixes allant du pico au méga, c'est-à-dire de 10^-12 à 10^6 .
Plus rarement nous emploierons le "giga" (10^+9 ) et le "téra"(10^+12 ), soit pour des fréquences élevées, soit pour des capacités de stockage en informatique : gigahertz, giga- ou téraoctet.
Revenons sur Terre :
(en notation scientifique)
La masse de notre planète vaut environ :
6 000 000 000 000 000 000 000 000 kg, soit 6 mille quadrillions de kilogrammes,
ce qui peut s'écrire :
6. 10^24 kg
OUF ! me voila un peu rassuré !
Sympa comme notation.
Ce nombre peut se prononcer 6 yotta kilogrammes et sera noté 6 Ykg.
Si je compare la masse de la Terre avec la masse de la Lune, soit environ 7,348×10^22 kg, je comprends tout de suite que la Lune est à peu près 100 fois moins lourde que la Terre.
En effet, le rapport entre 10^24 et 10^22 est tout bêtement 10 ^(24-22) = 10^2, soit 100.
Si j'exprime les deux masses comme ceci :
Terre : ≈ 6 000 000 000 000 000 000 000 000 kg
Lune : ≈ 7,3 480 000 000 000 000 000 000 kg
... c'est très nettement moins évident !
Retour sur le petit calcul inachevé du début :
Reprise de l'exemple :
-
la résistance vaut 12000000 ohms
-
elle est traversée par un courant de 0,000002 ampères (A)
⇒ quelle est la tension aux bornes de la résistance ?
Petit passage par les puissances de 10 :
-
la résistance vaut 12.10^6 ohms (12 mégohms ou 12 MΩ)
-
elle est traversée par un courant de 2.10^-6 ampères (2 microampères ou 2 µA)
On applique la loi d'Ohm : U=R x I :
U = 12.10^6 x 2.10^-6
U = 12 x 2 x 10^(6-6)
U = 24 x 10^0
U = 24 volts
Immédiat, clair, facile, sûr... et indispensable !
Pourquoi faire autrement ?
Voilà.
Il fallait que tout ceci fut dit.
Les calculs pratiques avec les puissances de 10 se feront soit dans les autres "topos" sur les composants, soit pendant les ateliers d'électronique organisés par Alain.

ÉLECTRONIQUE de BASE
Trois grandeurs INDISPENSABLE
... et suffisantes dans 95% des cas :
COURANT, TENSION, PUISSANCE
Ce sont les grandeurs FONDAMENTALES de l'électricité et donc de l'électronique.
Elles sont réunies dans une loi : la loi d'Ohm
P = U x I
P en watts, symbole W
U en volts, symbole V
I en ampères, symbole A
Note : Comme tous les noms d'unités du Système international, « watt » s'écrit en minuscules. En revanche, comme ce nom d'unité provient du nom patronymique d'un physicien, le symbole associé « W » est écrit en majuscule.
Ceci est vrai pour toutes les unités auxquelles on a donné le nom d'un scientifique.
Pour faire simple, on peut dire que :
-
une source qui génère dans un circuit un courant « I » sous une tension « U »,
délivre une puissance égale à P = U x I
-
une charge parcourue par un courant «I» qui provoque une tension U à ses bornes,
dissipe une puissance égale à P = U x I

Dans l'exemple théorique ci-dessus :
-
la source délivre une puissance P = Vcc x I
-
la Charge 1 dissipe (ou consomme) une puissance P1 = U1 x I
-
la Charge 2 dissipe (ou consomme) une puissance P2 = U2 x I
Sources électriques :
Il s'agit par exemple d'une alimentation filtrée de laboratoire ou de fabrication maison.
Dans le cas de montages embarqués dans les modèles réduits de trains, c'est par exemple la tension de traction présente sur les voies.
Charges :
Les types de charges sont innombrables :
-
résistances ;
-
LED ;
-
montage électronique complet ;
-
caméra embarquée ;
-
moteur (attention tout de même : un moteur ne se comporte jamais comme une charge résistive parfaite) ;
-
...
Cas d'un régulateur série :
Un régulateur de tension de type série (78xx par ex.) qui abaisse et régule une tension pour alimenter un montage peut AUSSI être considéré globalement et approximativement comme une charge.
En effet, ce type de régulateur se comporte comme une charge résistive pilotée, c'est à dire comme une résistance variable dont la valeur est instantanément assistée pour maintenir la valeur désirée de la tension de sortie.
Par conséquent, lorsqu'on détermine un régulateur, il faut :
-
choisir sa tension de sortie ;
-
vérifier qu'il supporte la tension d'entrée qu'on lui applique ;
-
vérifier qu'il supporte le courant consommé par le montage qu'il alimente ;
-
calculer la puissance qu'il dissipe : P = (tension d'entrée - tension de sortie) x courant consommé ;
-
contrôler que cette puissance est inférieure à la puissance maximale admissible ;
-
déterminer le radiateur nécessaire pour évacuer cette énergie et maintenir une température raisonnable.
... et ce n'est pas tout :
La puissance maximale admissible du régulateur (et par conséquent sa température maximale admissible) est donnée par le constructeur pour une température ambiante de 20 °C.
Si le régulateur est confiné dans un boitier ou un wagon..., c'est à dire s'il est mal ventilé, l'évacuation de l'énergie se fera mal et les températures atteintes seront plus élevées. Il y a risque de destruction du régulateur, ou... fusion du wagon !
Autrement dit on peut très bien avoir choisi le bon régulateur qui délivre la bonne tension et dont la capacité en courant est supérieure aux besoins, et avoir pourtant de sérieux ennuis avec le dégagement de chaleur du régulateur.
La charge est une LED :
La datasheet de ce composant indique entre autre :
-
la tension nominale en fonctionnement ;
-
le courant maximal admissible.
Il est donc aisé d'en déduire la puissance maximale consommée par cette LED :
P = ULED x ILED
Exemple : une LED dont la tension nominale est 2,3 volts et qu'on alimente sous 20 mA dissipe une puissance égale à :
P = 2,3 x 20 / 1000
P = 46 mW
Puissance dissipée par une résistance : effet Joule
Si est la valeur ohmique de la résistance, alors on a :
U = R x I
Cela conduit à l'expression de la puissance (2 formes possibles) :
P = R x I^2 = U^2 / R
ÉLECTRONIQUE de BASE
Note : ceci n'est pas un cours théorique.
Ici on ne traitera pas de la technologie des résistances, ni des associations de résistances, ni de la loi des noeuds, de la loi des mailles ou du théorême de Kirchoff !
Il s'agit simplement de faire comprendre ce qu'est une résistance, sans faire appel à des calculs plus compliqués qu'une simple règle de trois.
Table des matières :
-
Préambule
-
Unités
-
Représentations schématiques et notations
-
Gammes normalisées
-
Marquage et lecture
-
Constitution physique
-
Caractéristiques limites (puissance, stabilité, tension de claquage, tolérances...)
-
Mesures du composant
-
Types spéciaux
-
Une piste de circuit imprimé est une résistance !
-
Références internet
Préambule
Résistance = force d'opposition à la circulation d'un courant.
Ambiguïté
Par métonymie on emploie le mot « résistance » pour :
-
la VALEUR « ohmique » du composant ;
-
le composant lui-même.
C'est le seul composant qui entretient cette confusion.
On devrait désigner ce composant par « resistor » ou « résisteur » ou « dipôle résistant », et réserver le terme « résistance » à la valeur du composant.
On notera que les 2 autres composants fondamentaux ne confondent pas dans un même mot la valeur et le composant lui-même :
-
une bobine ou self (c'est son nom de composant) a une inductance de xxx henrys
-
un condensateur ou capacitance (c'est son nom de composant) a une capacité de yyy farads
(même si par abus de langage les électroniciens disent « une capa » pour désigner un condensateur, ou « une inductance » pour désigner une self ou une bobine).
Unité
L'unité de résistance est l'ohm, du nom d'un physicien allemand : Georg Simon Ohm.
Symbole : Ω
Comme tous les noms d'unités du Système international, « ohm » s'écrit en minuscules.
J'ajoute que, le cas échéant, « ohm » prend la marque du pluriel comme n'importe quel nom commun.
Représentations schématiques et notations


Sur un schéma, une résistance est désignée par « Rxx ».
Plusieurs notations peuvent être utilisées pour figurer sa valeur ohmique :
-
100 R pour 100 ohms
-
100 K pour 100 kiloohms (ou kilo-ohms)
-
1K5 pour 1,5 kiloohms
-
1M pour 1 megohm, avec ou sans accent sur le "e" (ou megaohm ou mega-ohm) = 1 million d'ohms
-
2M7 pour 2,7 megohms
-
1 R pour 1 ohm
-
0R33 pour 0,33 ohms
-
1R5 pour 1,5 ohms
⇒ dans le 3e exemple, la lettre «K» indique la position de la virgule ;
⇒ dans le 5e exemple, la lettre «M» indique la position de la virgule ;
⇒ dans les trois derniers exemples, la lettre « R » indique la position de la virgule.
Toutes ses notations sont nées de la nécessité, pour plus de clarté, d'économiser la place occupée sur les schémas par les différentes indications.
On n'écrit jamais :
-
1200 K, mais 1,2 M ou 1M2 ("M" pour "méga" indique la position de la virgule)
-
12000 R, mais 12K
Pour les très faibles valeurs de résistances (valeur de la résistance d'un contact par exemple) on utilisera :
-
le milli-ohm, ou milliohm, noté mΩ ;
-
le micro-ohm ou microohm, noté µΩ.
Gammes normalisées
Il faut se référer à l'excellent article ci-dessous :
http://fr.wikipedia.org/wiki/CEI_60063
Dans nos applications courantes, nous utilisons la gamme E12 qui comporte 12 valeurs pour chaque décade :
-
12 valeurs de 1 à 10 ohms (10 ohms non non inclus) ;
-
12 valeurs de 10 ohms à 100 ohms (100 ohms non inclus) ;
-
etc.
Marquage et lecture
Il existe sur le net de nombreux articles très bien faits, dont celui-ci :
http://webetab.ac-bordeaux.fr/Pedagogie/Physique/Physico/Electro/e07rtor.htm#Code%20des%20couleurs
Les résistances CMS étant bien plus petites, les constructeurs ont adopté un marquage chiffré :
http://fr.wikipedia.org/wiki/R%C3%A9sistance_%28composant%29
Le marquage « couleur » et le marquage « chiffré » sont parfaitement équivalents :
-
résistance à fils avec 3 anneaux de couleurs + 1 anneau séparé pour la valeur de la tolérance :
marron = 1 / rouge = 2 / orange = 3 ⇒ valeur 12kΩ (12 suivis de 3 zéros).
⇒ la résistance CMS correspondante sera notée « 123 » (12 suivis de 3 zéros).
-
résistance à fils avec 4 anneaux de couleurs (séries à faible tolérance de valeur) + 1 anneau séparé pour la valeur de la tolérance :
marron = 1 / rouge =2 / orange = 3 / jaune = 4 ⇒ valeur 1,23 MΩ (123 suivis de 4 zéros).
⇒ la résistance CMS correspondante sera notée « 1234 » (123 suivis de 4 zéros).
Code couleurs à 3 et 4 anneaux plus l'anneau de tolérance :
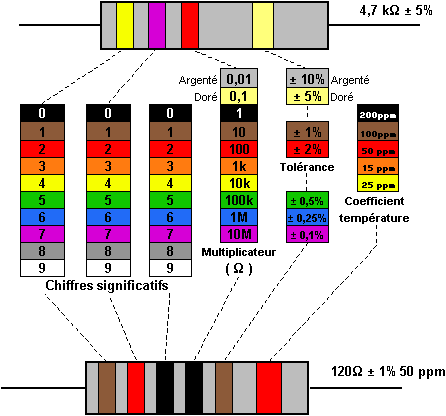

Cette image est issue de l'excellent article ci-dessous :
http://fr.wikipedia.org/wiki/R%C3%A9sistance_%28composant%29
Complément sur les résistances CMS :
Les résistances CMS sont marquées d'un code numérique à trois ou quatre chiffres.
-
avec le marquage à trois chiffres, les deux premiers représentent la valeur, le troisième est le multiplicateur en puissance de dix (ou plus simplement « le nombre de zeros » qui suivent les deux premiers chiffres). Pour les valeurs inférieures à 10 ohms la position du séparateur décimal est représenté par la lettre R.
-
avec le marquage à quatre chiffres, les trois premiers représentent la valeur, le quatrième est le multiplicateur en puissance de dix (ou plus simplement « le nombre de zeros » qui suivent les trois premiers chiffres). Pour les valeurs inférieures à 100 ohms la position du séparateur décimal est représenté par la lettre R.

N.B. le quadrillage mesure 1 millimètre !
_p.png)
Constitution physique des résistances :
http://joubert.marc.free.fr/1sti/technologie/composants_cms.pdf
-
agglomérées :
Ce sont d'anciennes fabrications actuellement quasiment disparues.
Elle sont instables dans le temps et à la température.Elles sont mal adaptées aux fréquences élevées.
-
couche de carbone :
Mêmes défauts que le type précédent, en moins pire.
-
couche métallique :
Beaucoup plus stables.Mieux adaptées aux fréquences élevées.
-
bobinées :
- en général ce sont des résistances de puissance (plusieurs Watts).
- elles présentent souvent une inductance résiduelle qui peut être gênante dans certaines applications.
- elles supportent des températures de fonctionnement élevées.
- elles doivent être ventilées.
-
avec un corps métallique :
Pour des résistances de forte puissance.
-
résistances CMS (SMD en anglais) :
La partie résistive est constituée d’une encre déposée par sérigraphie (oxyde de ruthénium) sur un substrat d'alumine qui est très stable en dimensions. La valeur de la résistance est ajustée par faisceau laser. Les terminaisons sont en barrière de nickel et assurent une excellente protection thermique au cours de l’opération de soudage ainsi qu’une bonne soudabilité.
Caractéristiques limites des résistances
Déterminer la valeur ohmique d'une résistance c'est bien.
Cela ne suffit pourtant pas à un bon usage du composant.
Voici deux cas très voisins à partir du même schéma électronique ci-dessous :

Il s'agit de déterminer la résistance qui alimente la LED.
Premier cas :
-
Vcc = 5 volts ;
-
Ud = 2 volts (tension aux bornes de la LED quand elle éclaire) ;
-
I = 20 mA (courant qui traverse la LED, donc le dipôle [R+LED]
Ur = Vcc - Ud
Ur = 5 - 2 = 3 volts
Application de la loi d'Ohm U = R x I avec U (volts) = R (ohms) x I (ampères) :
Ur = R x I ⇒ R = Ur / I
R = 3 V / 20 mA soit R = 3 / 20.10^-3
R = 3.10^+3 / 20
R = 3000 / 20
R = 150 ohms
=> cette valeur existe dans la série E12.
Note :
Au passage on remarque que dans l'expression « loi d'Ohm », le nom « Ohm » comporte une majuscule.
Tout simplement parce que dans cette expression, « Ohm » désigne le physicien, Monsieur Ohm, et non pas l'unité de résistance électrique.
Deuxième cas :
-
Vcc = 18 volts
-
Ud = 2 volts (tension aux bornes de la LED quand elle éclaire),
-
I = 20 mA (courant qui traverse la LED, donc le dipôle [R+LED]
Ur = Vcc - Ud
Ur = 18 - 2 = 16 volts
Application de la loi d'Ohm U=R x I :
Ur = R x I => R = Ur / I
R = 16 / 20 mA soit R = 16 / 20.10^-3
R = 16.10^+3 / 20
R = 16000 / 20
R = 800 ohms
⇒ cette valeur n'existe pas dans la série E12.
On choisira une résistance de 820 ohms.
Analyse :
Nos calculs sont exacts.
Et pourtant...
Il y a de fortes chances pour que la résistance de 820 ohms soit détruite en quelques secondes !
En effet, les résistances à fils les plus courantes, et que nous avons tous en stock, sont des modèles
« ¼ de watt » soit 250 milliwatts.
Ce sont des résistances « passe-partout ».
Mais parfois, ça ne passe pas !
Pourquoi ?
-
parce que TOUT COMPOSANT A DES LIMITES D'UTILISATION ou des domaines d'utilisation ;
-
parce que la valeur « ohmique » de la résistance N'EST PAS LE SEUL PARAMETRE IMPORTANT de ce composant.
Quelle est donc la caractéristique qui a conduit à la destruction de la résistance de 820 ohms alors que celle de 150 ohms a tenu ?
... c'est LA PUISSANCE MAXIMALE ADMISSIBLE, c'est à dire la puissance que la résistance est capable de dissiper sans être détruite ou altérée, dans des conditions ambiantes normales (température d'air ambiant 20°C).
Calcul de la puissance dissipée :
On utilise la relation P = U x I avec P en watts ; U en volts ; I en ampères
Premier cas : Ur = 3 volts aux bornes de la résistance
Pr = Ur x I
Pr = 3 x 20·10^-3
Pr = 60 mW, c'est à dire 60 milliwatts
La résistance de 150 ohms, DANS CE MONTAGE, dissipe 60 mW, ce qui est bien inférieur à sa limite de 250 mW.
Deuxième cas : Ur = 16 volts aux bornes de la résistance
Pr = Ur x I
Pr = 16 x 20·10-3
Pr = 320 mW, c'est à dire 320 milliwatts
La résistance de 820 ohms, DANS CE MONTAGE, dissipe 320 mW,
ce qui est bien supérieur à sa limite de 250 mW.
=> elle chauffe puis se détruit.
On constate donc que la détermination d'une résistance ne se borne pas à calculer sa valeur ohmique, mais AUSSI à vérifier sa puissance dissipée.
Que faut-il faire dans le deuxième cas ?
-
soit utiliser une résistance d'un modèle ½ Watt (500 mW) ;
-
soit utiliser une tension d'alimentation inférieure ;
-
soit utiliser deux résistances, de 390 ohms chacune, montées en série : chacune d'elle ne dissipera QUE 160 mW ;
-
soit faire fonctionner la LED avec un courant inférieur ;
Avec 10 mA par exemple : la résistance aura alors une valeur calculée de 1600 ohms (1500 ohms dans la série E12) et dissipera environ 160 mW ; -
soit utiliser un convertisseur continu-continu (voir ICI).
Remarque :
Il vous a sans doute sauté aux yeux que les calculs de puissance ci-dessus ne sont pas tout à fait exacts.
En effet quand on détermine une valeur de résistance de 800 ohms et qu'on choisit en réalité une résistance de 820 ohms (valeur la plus proche dans la série E12), il est bien évident que le courant RÉEL est légèrement différent et donc la puissance dissipée aussi.
Cela dit il est parfaitement stupide de recalculer les valeurs de courant et de puissance avec la valeur de 820 ohms au lieu de 800.
En effet, les résistances de la série E12 ont typiquement une tolérance de valeur de +/- 5 % :
-
une résistance marquée 820 ohms peut donc prendre des valeurs comprises entre 781 ohms et 861 ohms. La valeur de 800 ohms est comprise dans cet intervalle ;
-
une résistance marquée 1000 ohms peut prendre des valeurs comprises entre 952 ohms et 1050 ohms ;
-
etc.
En fait la résistance de 820 ohms n'est éloignée que de 2,5 % de la valeur théorique calculée de 800 ohms (dans notre exemple).
Autre remarque :
Il n'est pas raisonnable de flirter avec la limite de puissance d'une résistance. Il est fortement conseillé de garder une marge de sécurité confortable :
-
la température ambiante peut varier fortement (été, hiver, local chauffé...) ;
-
le température ambiante dépend aussi du fait que le montage est confiné ou pas, ventilé ou pas ;
-
les soudures de la résistance vieillissent prématurément si la température du composant est élevée.
Pire, les soudures peuvent fondre ; -
sur un montage, certains composants peuvent dégager de la chaleur et provoquer localement une élévation de température préjudiciable qui peut aller jusqu'à endommager un composant voisin (condensateur par exemple).
Autre remarque encore :
Est-il bien raisonnable de dissiper 320 mW en pure perte dans une résistance qui alimente une LED dont la consommation est 40 mW (2 volts x 20 mA) ?
Ne vaudrait-il pas mieux envisager une alimentation du dipôle sous 5 V ?
Conclusion :
Les calculs ci-dessus montrent à l'évidence que la prise en compte des paramètres physiques du composant est une tâche plus importante que le seul calcul de la valeur ohmique.
Autres valeurs limites d'une résistance :
-
la tension maximale d'utilisation ;
-
la tension maximale de surcharge ;
-
le temps et la température maximale de soudage sans modification de ses caractéristiques physiques et électriques ;
-
la tolérance de valeur (10 %, 5 %, 1%) ;
-
le coefficient de température, càd le taux de variation de la valeur de la résistance en fonction de sa température ;
-
la température maximale de fonctionnement ;
-
la résistance aux solvants ;
-
la résistance à l'humidité ;
-
etc., etc.
Ceci met en évidence le fait que, pour tout type de composant, il faut consulter les « datasheet » (feuilles de caractéristiques) éditées par les constructeurs et n'utiliser chaque composant que dans les limites prescrites.
Mesure d'une résistance
La mesure précise de la valeur d'une résistance s'effectue avec des appareils de laboratoires sophistiqués.
Le pont de Weatstone permet des mesures extrêmement précises.
Cependant, pour un usage « amateur » la plupart des multimètres ont une fonction de mesure des résistances suffisamment performante.
Des petits appareillages d'origine chinoise, avec afficheur graphique, réalisent aussi la mesure des composants de base (résistances, condensateurs, selfs, transistors, diodes,...), et cela de façon très conviviale pour un prix modique.
Mais, pour une résistance, quelles informations fournissent ces appareils ?
Uniquement la valeur « ohmique ».
Rien sur la dissipation maximale !
Rien sur la tension de service !
Rien sur le coefficient de température, etc. !
Et c'est bien là que réside toute la difficulté de mesurer une résistance inconnue : la mesure ne nous dit rien sur ses autres propriétés physiques que seuls des appareillages coûteux permettent de tester (et souvent de façon destructive).
On verra dans un autre chapitre qu'il en est de même pour tous les composants de base : la mesure nous informe sur la valeur « électronique » du composant et c'est tout.
D'où la nécessité de consulter les datasheets... j'insiste.
Types spéciaux de résistances
Il existe des types de résistances particuliers qui exploitent des caractéristiques qui serait considérées comme des défauts chez une résistance idéale :
-
sensibilité à la lumière ⇒ photo-résistance ;
-
sensibilité à la température ⇒ thermistance, thermocouple, bilame ;
-
sensibilité à la tension aux bornes ⇒ varistance ;
-
sensibilité à un champ magnétique ⇒ magnétorésistance ;
-
sensibilité à une contrainte mécanique ⇒ jauge de contrainte ou extensomètre, capteurs tactiles ;
-
sensibilité à l'oxygène ⇒ oxymètre (variation de conductibilité d'une céramique poreuse à base d'oxyde de zirconium (ZrO2) traversée par un flux d'oxygène) ;
-
sensibilité à l'humidité ⇒ capteurs résistifs au chlorure de lithium ;
-
sensibilité à la position ⇒ potentiomètre ;
-
sensibilité à une forte température ⇒ fusible et résistance-fusible ;
-
...
Hé oui, un fusible est une résistance :
Il est constitué d'un filament de métal qui présente une résistance calibrée pour fondre si le courant qui la traverse dépasse ou atteint une valeur déterminée.
Varistance : vous en connaissez au moins un type :
Il s'agit des lampes à filament de tungstène dont la résistance est faible à température ambiante et qui augmente lorsqu'elle est alimentée.
Une piste de circuit imprimé est AUSSI une résistance !
Le site suivant :
http://nononux.free.fr/index.php?page=elec-brico-outils#!elec-brico-outil-largeur-piste-pcb
... propose un calculateur de piste de circuit imprimé.
Étonnant :
Une piste de cuivre en épaisseur 35 µm, de largeur 0,3 mm et de longueur 30 mm représente une résistance de 50 mΩ.
Si cette piste est parcourue par un courant de 1 A, la chute de tension sera d'environ 50mV et la puissance dissipée (perdue) par cette portion de piste sera... environ 50 mW !
Fichtre !
Je suis certain que vous n'aviez pas vu les choses de cette façon !
Références internet :
http://fr.wikipedia.org/wiki/CEI_60063
http://webetab.ac-bordeaux.fr/Pedagogie/Physique/Physico/Electro/e07rtor.htm#Code%20des%20couleurs
http://fr.wikipedia.org/wiki/R%C3%A9sistance_%28composant%29
http://nononux.free.fr/index.php?page=elec-brico-outils#!elec-brico-outil-largeur-piste-pcb

That's all Folks !

IDENTIFICATION des CMS
CMS = Composants Montés en Surface.
SMD = Surface Mounted Divice



Abondance de biens ne nuit pas...
Voici 3 tables qui expliquent la codification des dimensions des composants CMS.
CLIC sur les images pour les agrandir.

1. Capacité Tantale boitier A (Dessous et Coté)
2. Capacité Tantale boitier D (Dessus et Coté)
3. Capacité électrolytique (Coté)
4. Capacité électrolytique (Dessous)
5. 0805 Céramique
6. 1206 Céramique
7. 1210 Céramique
8. High Q Porcelaine RF
9. Variable trimmer (Dessus et Dessous)

1. 1 Watt 1218
2. 1206 1/4 Watt
3. 0805 1/8 Watt
4. Potentiomètre (Dessus et Dessous)
Sur toutes ces images, la résistance filaire 1/4 watt donne l'échelle de taille.
Les valeurs sont codées comme suit :
-
Codage sur trois ou quatre chiffres :
-
Codage sur 3 chiffres :
2 premiers chiffres : valeur,
3ème chiffre : nombre de 0.
Exemples : 223 = 22 kΩ ; 101 = 100 Ω. -
Codage sur 4 chiffres :
3 premiers chiffres valeur,
4ème chiffre : nombre de 0.
Exemples : 1001 = 1kΩ.
-
-
Pour les faibles valeurs le 3ème chiffre peut être remplacé par R. Exemple : 56R = 56 Ω
-
Pour les trés faibles valeurs, le R est utilisé comme virgule entre le premier et le deuxième chiffre. Exemple : 5R6 = 5,6 Ω

1. DIP 20 pattes (pour comparaison)
2. SOIC 20 pattes (large)
3. SOIC 8 avec radiateur
4. SOIC 8
5. SSOP 20 pattes
1. transistor de puissance
2. Led CMS
3. MELF Diode (Metal Electrode Leadless Face :
face constituées par les électrodes métalliques sans fil)
4. SOT à 4 pattes
5. Diode SMB
6. SOT-223 3 pattes (transistor, régulateur, double diode...)




